はじめに
タイトルの通り、meshgridに関する覚書です。
普段はC++プログラマをやっていますが、プロトタイプを作成したり、ちょっと機械学習を試したりする時にはPythonを使います。
ライトユーザーとして、すぐに忘れてしまい何度も調べなおすことが多いので、備忘録として基本的な使い方を残しておきます。
np.meshgrid()とは
(直交)格子点を作成する時に使われます。永遠にPython素人をやっている私は、2次元の配列が2つ生成されていつも混乱します。
格子点の作成方法
1次元の配列を用意しておきます。これをnp.meshgridにいれてあげます。2次元配列が2つ返ってきます。
import numpy as np
x = np.arange(0, 1.01, 0.2) #0, 0.2, 0.4, 0.6, 0.8, 1.0
t = np.arange(0, 1.01, 0.5) #0, 0.5, 1.0
X, T = np.meshgrid(x, t)
print(X.shape)
print(T.shape)
print(X)
print(T)(3, 6)
(3, 6)
[[0. 0.2 0.4 0.6 0.8 1. ]
[0. 0.2 0.4 0.6 0.8 1. ]
[0. 0.2 0.4 0.6 0.8 1. ]]
[[0. 0. 0. 0. 0. 0. ]
[0.5 0.5 0.5 0.5 0.5 0.5]
[1. 1. 1. 1. 1. 1. ]]中身は、Xはtの要素数だけ行を拡張、Tはxの要素数だけ列を拡張したようになります。
よって、XとTのサイズは3×6となります。
こうすることで、XとTとセルの値をもつ配列(例えば、value)のサイズが一致するので同じ、要素番号で呼び出せるわけですね。
(x = 0.4, t = 0.5, value) = (X[2,1], T[2,1], value[2,1])となります。
利用例
1次元の熱伝導方程式を解いて、可視化時にmeshgridを使ってみます。
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# データの生成
L = 1.0 # 計算領域の長さ
T = 1 # 計算時間
N = 20 # 空間分割数
dt = 1.0e-2 # 時間刻み
x = np.linspace(0, L, N) # 空間グリッド
t = np.arange(0, T, dt) # 時間グリッド
# パラメータと初期条件。初期条件はガウシアン
alpha = 0.01
mu = L * 0.5
sigma = 0.2
u0 = np.exp(-(x - mu)**2 / sigma**2)
# 拡散方程式: u_t = alpha * u_xx
def compute_rhs(u, x, alpha):
ux = np.gradient(u, x)
uxx = np.gradient(ux, x)
return dd * uxx
# 時間発展の解を保存するための配列を用意
nt = len(t)
u_all = np.empty((nt, len(x)))
u_all[0] = u0.copy()
# オイラー法による時間積分
u = u0.copy()
for i in range(1, nt):
u = u + dt * compute_rhs(u, x, dd)
u_all[i] = u
# meshgridを利用: Xは空間、T_meshは時間
X, T_mesh = np.meshgrid(x, t)
print(u_all.shape)
# contourfを使って拡散方程式の時間発展をプロット
plt.figure(figsize=(8, 6))
contour = plt.contourf(X, T_mesh, u_all, levels=50, cmap='rainbow')
plt.colorbar(contour, label='u value')
plt.xlabel('Space (x)')
plt.ylabel('Time (t)')
plt.title('Diffusion Equation')
plt.show()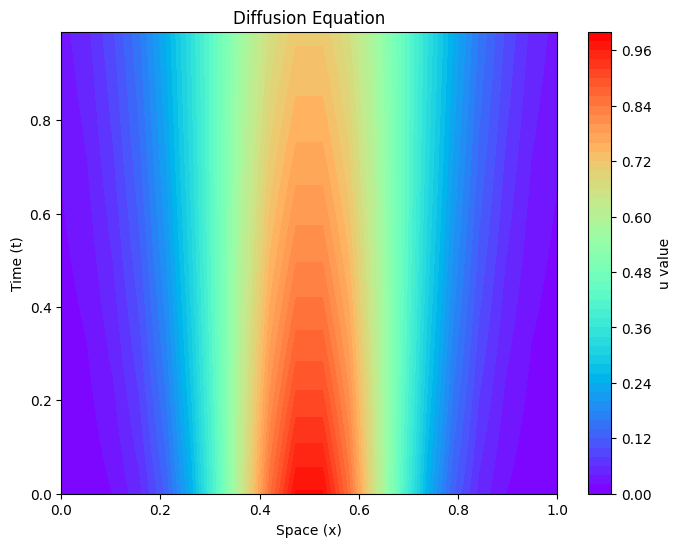
meshgridを用いて可視化できました。
今回は、以上です。最後までよんでいただきありがとうございました!

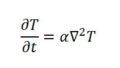
コメント